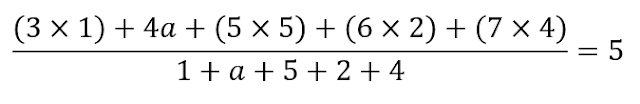Resourceaholic: Symmetry

This is the seventh short article composed in the ‘Dose of Don’ collection – this just one is created by Sudeep Gokarakonda (@boss_maths). Anne Watson posted it on her blog here and I have replicated it phrase for phrase. For the qualifications on this collection, please see the post Lines and Angles on Sq. Grids. My many thanks go to Sudeep for providing me authorization to share his creating here.

Dose of Don 7: Symmetry

This is a contribution to sequence of writings, started by Anne Watson, which delve into the selection of jobs on Don Steward’s blog and pull out threads about key tips in arithmetic that operate through various of his responsibilities. Direct back links to all duties pointed out are incorporated underneath.

Don was extremely generous with his duties and it is hoped that you will return this generosity in the way he requested prior to he died, specifically to donate to justgiving.com/fundraising/jessesteward.

This publish is about symmetry. Mention symmetry, and a lot of people’s very first ideas may well contain symmetry in a firmly geometric context. At school, pretty much all pupils explicitly face reflection and rotational symmetry. For numerous, their appreciation of symmetry could not lengthen further than these ideas.

Symmetry is anything that permeates arithmetic, and it is something mathematicians can recognise in conditions that are not presented in a regular geometric context. Listed here, for example, is this kind of a problem:

You have the adhering to cash totalling 70 pence. In these questions, “amount” refers to a whole number of pence.

a) Making use of only these cash, what is the smallest total you cannot make?

b) Making use of only these cash, what is the biggest total under 70 pence that you simply cannot make?

c) What do you observe about your two answers?

*****

I remember a lesson involving Pascal’s triangle during which I causally outlined its symmetry. A person scholar appeared convinced that I was wrong to suggest any symmetry right here. On exploring, I realised they were taking into consideration the numerals fairly than the figures, so for them:

This somewhat constrained conception of symmetry was not entirely surprising, figuring out that the student’s publicity to the notion had been constrained to the geometric contexts in the GCSE specification.

In this article are some slides from Don’s responsibilities. Not one particular of the selected duties is primarily about symmetry. Nonetheless, each and every provides us opportunities to observe and take a look at symmetry.

These are the initially two slides from the process. Let’s contemplate dilemma 16. The frequencies y, w, y, w, y read the same forwards and backwards. It is achievable to prove that the necessarily mean is often 6 with out recognizing this, by environment up and simplifying the pursuing:

But spotting the symmetry leads to a prospect to generalise. In dilemma 16, if I replaced y, w, y, w, y with any symmetric sequence (e.g.) a, b, c, b, a, would the signify continue to be 6? If the frequencies have been alternatively a, b, c, d, a but the imply was still 6, what could we conclude?

I also like tying query 16 back to queries 1 and 2 using an substitute strategy – appreciating how scores beneath the suggest should be flawlessly “balanced out” by scores earlier mentioned the indicate.

For illustration, in question 1, given that the signify is 5,

the solitary rating of 3 gives a “deficit” of 2
the scores of 5 have no impression on the necessarily mean
the two scores of 6 give a “surplus” of 2 and
the four scores of 7 give a “surplus” of 8.

Overall, I for that reason even now have to have a more “deficit” of 8. Given that a solitary rating of 4 effects in a deficit of 1, I need to have eight such scores, so a = 8.

This tactic is, to me, is mentally less taxing than location up and solving the next in my head:

The “balancing out” technique of system is effective in all issues, but it’s probably most effective illustrated working with those concerns where by the signify is an integer (i.e. concerns 1, 2 and 16), because the arithmetic is kept somewhat basic. I like how this part of the process can be bookended in this way.

The line y = x is a line of symmetry on all 4 slides – even where we only have the initial quadrant. This line of symmetry may possibly not to begin with be obvious to all students. On the pretty initially slide, nonetheless, is the possibility to place that e.g. (1, 12) and (12, 1) (2, 6) and (6, 2) etcetera. are all factors on the hyperbola. Is it necessarily the circumstance that if (a, b) is on the curve, then so is (b, a)? What about (–a, –b)?

These inquiries entail symmetry in a geometric context, but an possibility to think about symmetry in a far more refined context pops up on slide 4. I see that 3y + x = 12 is just y + 3x = 12 with the x and y swapped all over. With out even seeing the graphs of these, I sense symmetry in these coefficients. Below is an option to ask what happens, in normal, to a graph if I swap x and y around in its equation. Pupils could make predictions, and then look at by making an attempt a number of capabilities using graphing software program. Can they occur up with an intuitive rationalization for what they observe?

This instant may perhaps be a all-natural just one to consider a detour to pay a visit to (or revisit) self-inverse functions—or even sample one more of Don’s responsibilities, these kinds of as self-inverse and periodic features.

Visualising
The idea of symmetry crops up when contemplating arrangements, chances, and quite a few subjects in data. Don’s responsibilities frequently contain stunning but simple visualisations illustrating symmetry:

What I like in this final diagram is that, as drawn, it does not have rotational or reflective symmetry. This opens the likelihood to go over what mathematicians could possibly mean when conversing about symmetry here. These conversations should hopefully help broaden the type of conception of symmetry exhibited by my aforementioned college student of Pascal’s triangle.

*****

As mentioned before, none of the higher than jobs are primarily about symmetry. Don established other tasks that I’ve not in-depth right here, wherever it is pretty probable to operate through them – and attain richly – with no recognizing the symmetries in them. But spotting them presents lessons the opportunity to probably consider a “scenic route” by means of the duties – 1 that allows make up students’ sense of symmetry in arithmetic.